Что такое топологическая сортировка и где она применяется

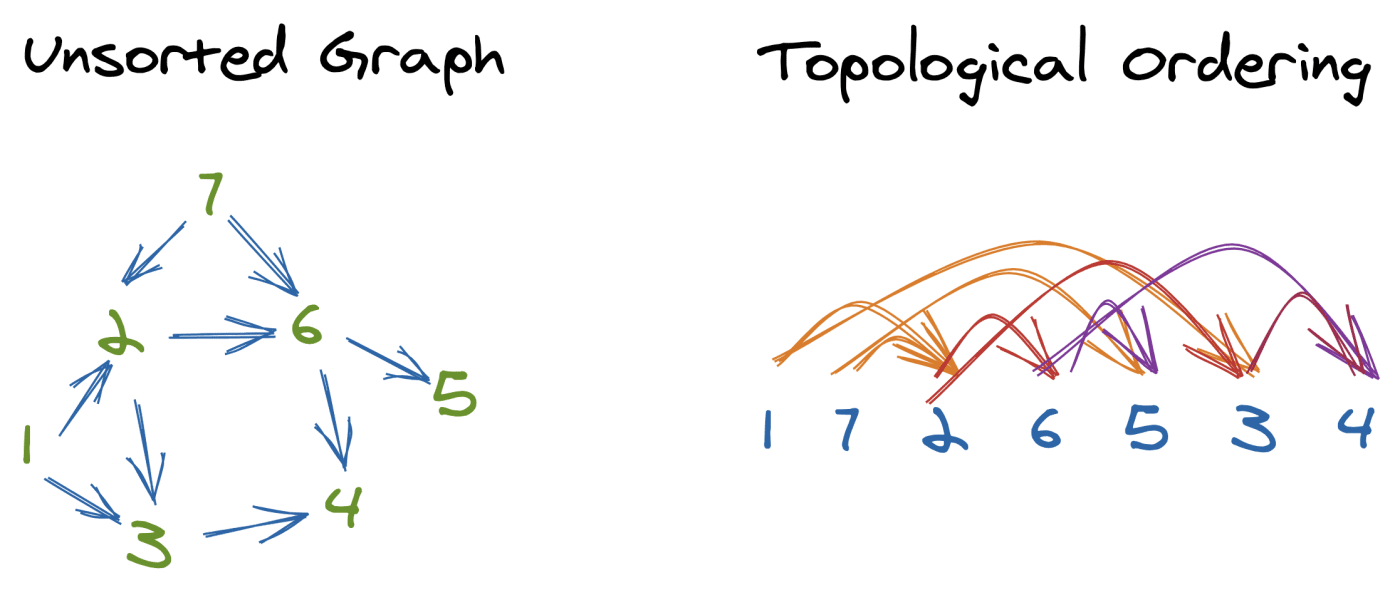
В мире графов существует множество интересных задач, но одна из самых полезных и широко применяемых — топологическая сортировка. Это фундаментальное понятие в теории графов, которое лежит в основе множества прикладных задач: от планирования проекта до сборки программного кода и анализа зависимостей. В этой статье мы подробно разберём, что такое топологическая сортировка, когда её можно использовать, какие есть алгоритмы её построения, и каковы реальные примеры применения.

Что такое топологическая сортировка

Топологическая сортировка — это линейное упорядочивание вершин ориентированного ациклического графа (ОАГ), при котором для каждого ребра (u → v) вершина u предшествует вершине v в полученной последовательности.

Проще говоря, если одна вершина зависит от другой (например, одна задача должна быть выполнена до другой), то в топологическом порядке зависимая вершина будет стоять позже.

Пример:

Предположим, у нас есть четыре задачи:

• A → B (B зависит от A)
• A → C
• B → D
• C → D

Возможный результат топологической сортировки: A, B, C, D или A, C, B, D. Главное — B и C идут после A, а D — после и B, и C.

Когда можно применять топологическую сортировку

Топологическая сортировка применима только к ориентированным ациклическим графам (DAG — Directed Acyclic Graph). Если в графе есть цикл (например, A зависит от B, B от C, а C от A), то корректная линейная зависимость невозможна, и топологическую сортировку построить нельзя.

Где используется топологическая сортировка

Топологическая сортировка широко используется во многих сферах:

1. Планирование задач и процессов

Допустим, вы разрабатываете проект, в котором одни задачи не могут начаться до завершения других. Например, перед тем как красить стены, нужно их построить. Топологическая сортировка позволяет определить корректный порядок выполнения всех задач с учётом зависимостей.

2. Сборка программных проектов

В больших программных системах модули часто зависят друг от друга. Например, библиотека A использует B, а B — C. Компилятор должен знать, в каком порядке собирать модули, чтобы не получить ошибок. Именно здесь применяется топологическая сортировка.

3. Управление зависимостями в пакетных менеджерах

Такие системы, как npm, pip, apt и другие, используют топологическую сортировку для установки пакетов в правильном порядке — сначала устанавливаются зависимости, потом зависящие от них пакеты.

4. Анализ учебных программ

Если предмет «Алгебра» требует предварительного изучения «Математического анализа», то при построении плана обучения нужно учитывать эти зависимости. Топологическая сортировка поможет определить, в каком порядке нужно изучать дисциплины.

Как работает топологическая сортировка

Существует два основных алгоритма построения топологической сортировки:

1. Алгоритм Кана

Принцип работы:

1. Находим все вершины с нулевой входящей степенью (то есть те, от которых ничего не зависит).
2. Добавляем их в очередь.
3. Удаляем вершину из графа, уменьшая входящие степени её соседей.
4. Повторяем процесс до тех пор, пока не обработаем все вершины.

Если в процессе остаются вершины с ненулевой входящей степенью, значит, в графе есть цикл — топологическая сортировка невозможна.

Преимущества: простой и эффективный алгоритм, хорошо подходит для реализации.

2. Алгоритм на основе поиска в глубину (DFS)

Принцип работы:

1. Обходим граф в глубину.
2. После обработки всех соседей вершины добавляем её в стек.
3. Финальный порядок — это обратный порядок извлечения из стека.

Этот метод особенно популярен из-за своей лаконичности и простоты реализации в рекурсивной форме.

Пример реализации на Kotlin

Вот пример реализации топологической сортировки на языке Kotlin с использованием алгоритма Кана:

import java.util.*

fun topologicalSort(graph: Map<String, List<String>>): List<String> {
    val inDegree = mutableMapOf<String, Int>()
    val result = mutableListOf<String>()

    // Инициализация входящих степеней
    for (node in graph.keys) {
        inDegree[node] = 0
    }
    for ((_, neighbors) in graph) {
        for (neighbor in neighbors) {
            inDegree[neighbor] = inDegree.getOrDefault(neighbor, 0) + 1
        }
    }

    // Очередь вершин с нулевой входящей степенью
    val queue: Queue<String> = LinkedList()
    for ((node, degree) in inDegree) {
        if (degree == 0) {
            queue.add(node)
        }
    }

    // Основной цикл сортировки
    while (queue.isNotEmpty()) {
        val current = queue.remove()
        result.add(current)

        for (neighbor in graph.getOrDefault(current, emptyList())) {
            inDegree[neighbor] = inDegree[neighbor]!! - 1
            if (inDegree[neighbor] == 0) {
                queue.add(neighbor)
            }
        }
    }

    // Проверка на наличие цикла
    if (result.size != graph.size) {
        throw IllegalArgumentException("Граф содержит цикл, сортировка невозможна")
    }

    return result
}

// Пример использования
fun main() {
    val graph = mapOf(
        "A" to listOf("B", "C"),
        "B" to listOf("D"),
        "C" to listOf("D"),
        "D" to emptyList()
    )

    val sorted = topologicalSort(graph)
    println("Топологическая сортировка: $sorted")
}

Что делать, если в графе есть цикл?

Если вы попытаетесь построить топологическую сортировку в графе с циклом, алгоритм обязательно даст сбой. Циклы говорят о логической ошибке в постановке зависимостей. Например, если задача A зависит от B, а B от A, то их нельзя упорядочить линейно — нужно изменить структуру зависимостей.

Заключение

Топологическая сортировка — это мощный инструмент для работы с зависимостями в самых разных областях. Она помогает находить корректный порядок действий, строить эффективные планы и избегать логических ошибок. Главное условие — отсутствие циклов в графе. С помощью простых алгоритмов (например, алгоритма Кана или DFS) можно легко и быстро упорядочить даже крупные графы с десятками и сотнями элементов.

Если вы работаете с системами зависимостей, планированием, компиляцией или просто хотите лучше понимать графовые алгоритмы — такая сортировка будет для вас незаменимым инструментом.